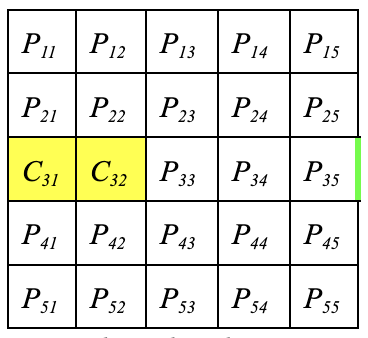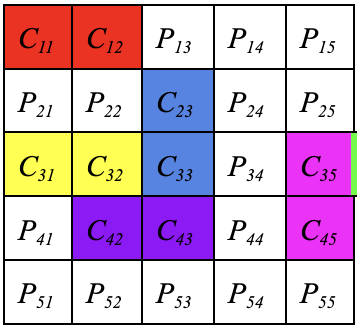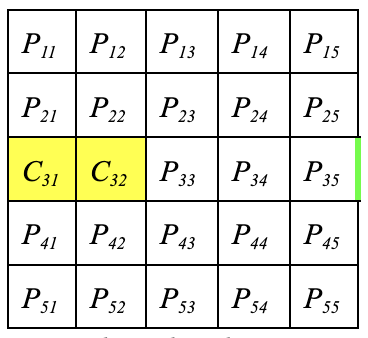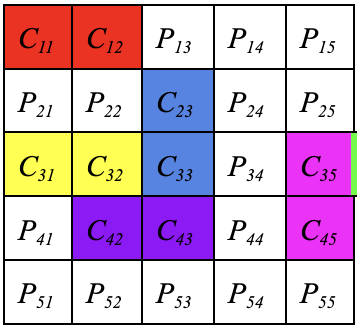The kids game Rush Hour involves a map for each game that dictates where to place each car. The goal is to move the cars around the board in order to free a path for the winning car to exit the board.
Cars take up two adjacent cells, either horizontally or vertically, and move along the axis in which their two cells are adjacent. The solution to any given board, if it exists, can be modeled by a sequence of car movements until there is either a clear path for the winning car to exit, or it is deemed unsolvable.
I will model the order of these required movements on a simplified game board from the original car placement to the final arrangement when the winning car is free. To do this, I will set constraints on all car movements to eventually be able to compute which movements are possible, test them, and assess which sequence of movements result in a solved or declared unsolvable board.
Simplified board: 5x5 board, 4 cars + winning car, the winning car always starts directly across the board from the exit oriented horizontally (C_31,C_32). As opposed to the real game, the board may not necessarily be solvable.
Fig 1: Empty board with winning car and exit, Fig 2: Example board with cars
Propositions:
• P_rc is true for (1 ≤ r ≤ 5 ^ 1 ≤ c ≤ 5)
• C_rc is true if a car exists at row r and column c
• V_ds is true when a car oriented vertically is able to move s spaces in d direction
•H_ds is true when a car oriented horizontally is able to move s spaces in d direction
Constraints:
Between each game state (grid specifying the two positions of each car and the exit as displayed above) there is one car movement.
• A car can move forwards or backwards along its given axis: C_(r + s c) or C_(r c + s) forwards, or C_(r - s c) or C_(r c - s) backwards
• A car cannot be oriented in two directions at the same time: For a given car C, ~(C_rc ^ C_(r + 1 c + 1))
• Only one car can move at a time: |{C_rc ^ ~(C_(r + 1 c + 1)}| = 1
• A car can’t move s spaces if another car is blocking the same row/col between its desired position and its current position: C_(rc + s) → ~(V_ds) or C_(r + s c)→ ~(H_ds)
• A car can’t move s spaces forward or backwards if grid space s + 1 doesn’t exist (a wall is reached): ~(P_(r c+ s)) → ~(V_ds) or ~(P_(r + s c)) → ~(H_ds)
Limitations:
My model assumes the given board is formulated correctly, and thus does not account for the event in which a car is placed in the winning car’s position (P_31 P_32) or any other cars are overlapping when the game board is generated. It additionally does not account for the scenario in which a non-winning car leaves the board through the exit. To improve upon my model and address these limitations, the next step would be to add similar constraints to car movement on the generation of the original board to disallow any car overlap. As well it would be necessary to address the possibility of a car exiting the board, and thus being removed from any future car movements (the car off the board cannot move nor return to the board). This could be achieved by removing the existence of the car once it has exited, its movements being recorded but not being included in any further game states.